Call: 708-425-9080
Vacuum Technology – Three Useful Terms Explained
Vacuum systems are used in many industrial and research applications, such as the manufacture of semiconductors used in electronic devices, and to provide the insulating vacuum in cryogenic systems that minimizes the incursion of thermal energy from external sources. When working with or specifying vacuum system components, the following three terms are important in characterizing the performance of individual components and the system as a whole. These terms are Pumping Speed, usually denoted by S, Throughput, usually denoted by Q, and Conductance, usually denoted by C. Understanding the difference in these terms gives useful insight into the operating envelope of an existing system or will generally be necessary in the design of a new vacuum system.
Pumping Speed, S
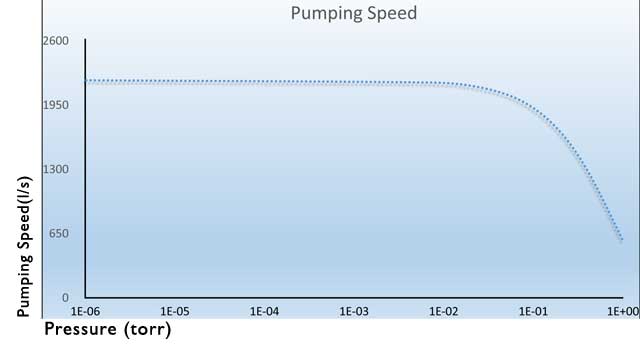
Pumping speed is an empirically determined performance characteristic of a vacuum pump and is defined as a volumetric flow rate across a plane at the pressure measured at the plane. The dimensions describing pumping speed are volume per unit time. Pumping speed is a function of the gas that is being pumped and the pressure at the plane used to define the pumping speed. Vacuum pump manufacturers use standard, well established techniques to measure the pumping speeds of their products. The accuracy of the techniques is thought to be very dependent on the specifics of the testing apparatus, so results among different manufacturers may not be comparable. Figure 1 is an example of what a pumping speed curve looks like for a turbomolecular pump and a single gas. Multiple gasses will have multiple curves on the plot.
Pumping Speed, S
Pumping speed is an empirically determined performance characteristic of a vacuum pump and is defined as a volumetric flow rate across a plane at the pressure measured at the plane. The dimensions describing pumping speed are volume per unit time. Pumping speed is a function of the gas that is being pumped and the pressure at the plane used to define the pumping speed. Vacuum pump manufacturers use standard, well established techniques to measure the pumping speeds of their products. The accuracy of the techniques is thought to be very dependent on the specifics of the testing apparatus, so results among different manufacturers may not be comparable. Figure 1 is an example of what a pumping speed curve looks like for a turbomolecular pump and a single gas. Multiple gasses will have multiple curves on the plot.
Throughput, Q
Throughput is defined as the volume of gas moving through a plane, per unit time, multiplied by the pressure at the plane, and is also known as Gas Load. Thus throughput, Q, is equal to Pressure*Volume/time, which leads to the useful relationship between throughput and pumping speed, Q=P*S. Throughput is proportional to the mass flow rate at a constant temperature. With substitution from the ideal gas law, PV = nRT, Q becomes nRT/t, where n is the quantity of gas in moles, R is the ideal gas constant, and T is the temperature of the gas, we see that Q is proportional to T, temperature and n, the molecular quantity (moles) of gas particles. Furthermore, as pressure multiplied by volume has the same units as energy; throughput can be thought of as the flow of energy per unit time. Power is defined as energy per unit time, thus throughput gives an idea of the power required for the system. A typical throughput curve is shown contrasting with pumping speed in Figure 2.
Conductance, C
Conductance is the volumetric capacity of gas flow in a passive component, or aggregate components, of a vacuum system, such as an opening or a pipe, divided by time. Thus the dimensions that describe conductance are the same as pumping speed, volume per unit time, but conductance is a phenomenon usually used to describe piping and openings, generally not the vacuum pump. Conductance in a vacuum system is analogous to conductance (inverse of resistance) in an electric circuit. Parallel conductance is the sum of each conductance: Ctotal = C1 + C2+…..Cn and series conductance is the inverse of the sum of each inverse conductance: 1/Ctotal = 1/C1 + 1/C2+…..1/Cn. Low conductance can significantly reduce the effective pumping speed, Seff, of a vacuum pump with the effective pumping speed defined as 1/Seff = 1/S +1/C. Conductance becomes increasingly important as the pressure moves below 1x10e-2 Torr where the flow transitions from a viscous regime, where particle – particle interaction of gas molecules is significant, to a molecular regime, where little particle – particle interaction exists.
Understanding how to utilize these concepts in the design of new equipment and systems is just one way Meyer Tool can help our customers reduce project risk and achieve the lowest total cost of ownership.
Further Reading
Throughput is defined as the volume of gas moving through a plane, per unit time, multiplied by the pressure at the plane, and is also known as Gas Load. Thus throughput, Q, is equal to Pressure*Volume/time, which leads to the useful relationship between throughput and pumping speed, Q=P*S. Throughput is proportional to the mass flow rate at a constant temperature. With substitution from the ideal gas law, PV = nRT, Q becomes nRT/t, where n is the quantity of gas in moles, R is the ideal gas constant, and T is the temperature of the gas, we see that Q is proportional to T, temperature and n, the molecular quantity (moles) of gas particles. Furthermore, as pressure multiplied by volume has the same units as energy; throughput can be thought of as the flow of energy per unit time. Power is defined as energy per unit time, thus throughput gives an idea of the power required for the system. A typical throughput curve is shown contrasting with pumping speed in Figure 2.
Conductance, C
Conductance is the volumetric capacity of gas flow in a passive component, or aggregate components, of a vacuum system, such as an opening or a pipe, divided by time. Thus the dimensions that describe conductance are the same as pumping speed, volume per unit time, but conductance is a phenomenon usually used to describe piping and openings, generally not the vacuum pump. Conductance in a vacuum system is analogous to conductance (inverse of resistance) in an electric circuit. Parallel conductance is the sum of each conductance: Ctotal = C1 + C2+…..Cn and series conductance is the inverse of the sum of each inverse conductance: 1/Ctotal = 1/C1 + 1/C2+…..1/Cn. Low conductance can significantly reduce the effective pumping speed, Seff, of a vacuum pump with the effective pumping speed defined as 1/Seff = 1/S +1/C. Conductance becomes increasingly important as the pressure moves below 1x10e-2 Torr where the flow transitions from a viscous regime, where particle – particle interaction of gas molecules is significant, to a molecular regime, where little particle – particle interaction exists.
Understanding how to utilize these concepts in the design of new equipment and systems is just one way Meyer Tool can help our customers reduce project risk and achieve the lowest total cost of ownership.
Further Reading
- O’Hanlon, John F. A User’s Guide to Vacuum Technology, Second Edition. New York: John Wiley & Sons, 1989.
- Varian Associates, Inc. Basic Vacuum Practice, Second Edition. Palo Alto: Varian Associates, 1989.
- Roth, Alexander. Vacuum Technology. New York: North-Holland, 1976.